Пример
3.3.1. (КубГУ, матем., 1990 г.).Решить неравенство
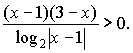
Решение:
Область допустимых значений определяется из соотношений
|
|
|||||
|
Функция |
|
обращается в ноль в точке x = 3 . |
|||
|
Заметим, что в силу сформулированного выше утверждения функции f(x) и |
|||||
|
|
на ОДЗ имеют одинаковые знаки. |
||||
|
Таким образом, в ОДЗ выделяются интервалы знакопостоянства |
|||||
|
|
Отметим их на вещественной оси, расставим |
||||
|
на них знаки функций g(x) , а значит и f(x), и выпишем ответ. |
|||||
|
Ответ: |
|
||||