Содержание раздела Разобранные примеры Задачи для самостоятельного решения

Пример 2.  Решить уравнение

. (2)

Решение

В этом уравнении контрольным является значение a=2. При a=2 уравнение (2) является линейным, а при  оно квадратное (в этом и состоит качественное изменение уравнения).

1) При a=2 уравнение (2) принимает вид -4x+1=0, решением которого будет x=1/4.

2) Из множества значений параметра  выделим те значения, при которых дискриминант уравнения (2) обращается в ноль, т.к. при этих значениях дискриминант может изменить знак, а также при них меняется число корней квадратного уравнения. Следовательно, можно говорить о качественном изменении уравнения.

Вычислим дискриминант уравнения (2):

, т.е. .

Из уравнения  находим второе и третье контрольные значения параметра a=1, a=6.

При этом, если , то D<0 и уравнение (2) не имеет корней. При a=1 ; при a=6 ; при .

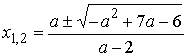Ответ: 1) если , то корней нет;

           2) если a=2, то x=1/4;

          3) если a=1, то ; если , то ;

         4) если , то .
 

Содержание раздела Разобранные примеры Задачи для самостоятельного решения