Содержание раздела Разобранные примеры Задачи для самостоятельного решения

Пример 7. Решить уравнение

. (7)

Решение

Уравнение (7) равносильно следующей системе

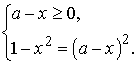
После преобразований получим

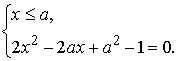(8)

Вычислим дискриминант полученного уравнения .

Корни уравнения ,  будут контрольными значениями. Систему (8) будем решать в каждом из следующих случаев:

1) ; 2) ; 3 ) ; 4) .

1) Если , то дискриминант квадратного уравнения в системе (8) отрицательный и, следовательно, уравнение (7) решений не имеет.
2) Если , то квадратное уравнение в системе (8) будет иметь решение 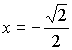, но это решение не удовлетворяет условию , следовательно, и в этом случае уравнение (7) решений не имеет.
3) Если , то 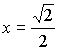 и условие  выполняется, следовательно, при  уравнение (7) имеет решение .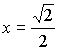

4) Если , то квадратное уравнение (8) будет иметь два корня , .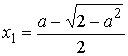

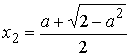Проверим, при каких значениях параметра a корень  удовлетворяет условию . Рассмотрим неравенство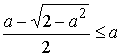
 

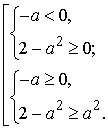
В результате получаем, что решением рассматриваемого неравенства будут . Следовательно, при  значение  будет корнем уравнения (7).

Проверим, удовлетворяет ли условию  значение . Рассмотрим неравенство

.
 

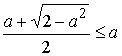
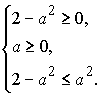
Таким образом,  – корень уравнения (7), если параметр a удовлетворяет условию .

Ответ: 1) если , то решений нет;

           2) если , то ;

          3) если , то два корня

, .

          4) если , то .
 

Содержание раздела Разобранные примеры Задачи для самостоятельного решения